Anisotropy analysis is the study of whether spatial pattern differs along different cardinal axes, for example, is the same pattern found along a North-South bearing as along an East-West bearing. Many of the methods already described have special anisotropic variants; additional methods are described in this section. Anisotropy analysis does not logically apply to one-dimensional data, but can be examined in both two and three dimensions.
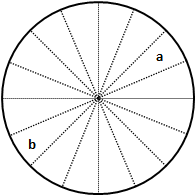
One typically examines two-dimensional anisotropy by either dividing space into equal sized sectors (in the figure below, space has been divided into 16 equal width segments) or by using a set of fixed bearings. In both cases, one does not normally try to distinguish between, for example, East to West vs. West to East, and therefore combines analysis from sectors separated by 180°. In the figure, therefore, there would only be 8 tested directions/sectors.
 |
 |
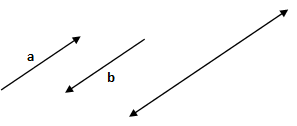
Dividing two-dimensional space into sixteen equal-sized sectors (22.5° each, in this case). Analysis from sectors a and b would be combined to form a single value because one is not normally trying to distinguish a specific direction (arrow a or arrow b) but rather a generalized bearing oriented along the a-b axis.
Three-dimensional anisotropic analysis is not as straight forward as two-dimensional analysis; one cannot simply divide three dimensional space into equal size sectors along both the θ and φ axes: recall that a 10° × 10° sector of latitude and longitude encompasses a very different area near the equator than near the pole. The solution is to not use the θ and φ axes directly, but instead to divide the sphere using a special tessellation in which each "tile" is a spherical triangle encompassing the identical surface area/volume and which can be perfectly applied to a hemisphere (allowing for symmetry, as found in the two-dimensional case shown above). There are a number of tessellations that fulfill these requirements: PASSaGE contains one built-in 3D spherical tessellation based on dividing the sphere with great circles at 45° separation. This produces 48 triangles around the full sphere, 24 in each hemisphere. This scheme is used in PASSaGE as the basis for 3D anisotropic analysis.
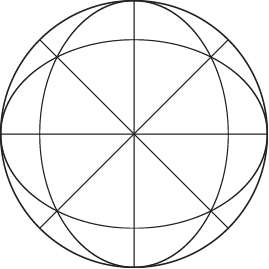
Dividing the sphere into equal area tessellations using spherical triangles. Each line is part of a great-circle separated from the others by a 45° rotation. There are 24 spherical triangles shown, with 24 additional symmetrical triangles on the opposite side of the sphere. If seen in full 3D, each triangle encompasses the identical surface area making this form of a tessellation ideal for subdividing three-dimensional space for anisotropic analysis.