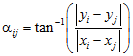
Angle calculations apply to two and three-dimensional coordinates. Angles can be used in a number of procedures for detecting variation of spatial pattern with direction or anisotropy. PASSaGE stores all angles internally as radians, but converts to degrees in the output for simpler interpretation in most analyses.
For Euclidean measures in two-dimensions, the angle is calculated as
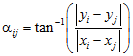
and then converted via symmetry to an angle between 0 and π. For latitudes and longitudes, the calculation of the spherical angle is much more complicated (equations not shown). Because of the curvature of the sphere, rather than calculating the angle directly between the two points, α is calculated between one of the points and the midpoint of the great circle arc connecting the points.
For three-dimensional coordinates, the first angle, θ, is exactly equivalent to the two-dimensional angle described above, except that it is measured around the full circle, from 0 to 2π. The second angle, φ, is measured as
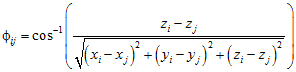
and then converted via symmetry to an angle between 0 and π/2.