3 dimensions
The distances between the points can be calculated either as Euclidean (rectangular) distances or spherical (geodesic) distances. Euclidean distances represent the straight-line distance between two points. If the coordinates of point i are xi (and yi and zi depending on the number of dimensions) the Euclidean distance between points i and j is:
| 1 dimension | |
| 2 dimensions | |
3 dimensions |
For one-dimensional elliptical plots, points are considered to be on the circumference of a circle and the distance between a pair of points is calculated as the minimum of the distances measured in both directions along the circle.
(A)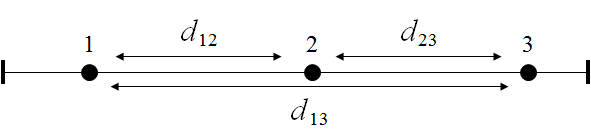
(B)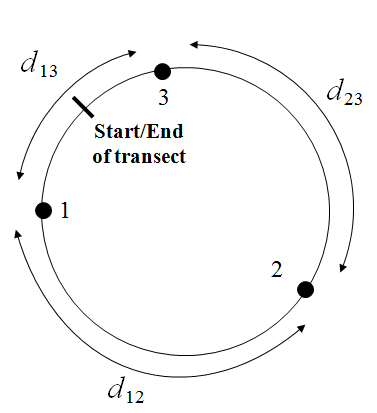
Calculating distances among points in one-dimensional elliptical plots. (A) A linear plot with three points and the distances among them. (B) The same plot as a circle. The distances from points 1 to 2 and 2 to 3 are the same, but the distance between points 1 and 3 is different because there is a shorter path through the (arbitrary) endpoints of the transect versus that along its entire length.
In two-dimensions, spherical distance can be calculated only from longitude and latitude coordinates. This distance is more accurate for points spaced around the globe and is calculated as the great circle distance along the surface of the Earth. If xi and yi are the longitude and latitude of point i, the spherical distance between points i and j is calculated as
![]()
![]()
where RE is the radius of the Earth (RE = 6379.336847km). Spherical distances are measured in kilometers.