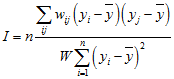,The metric proposed by Moran (1950) is commonly used in correlogram analysis. It is calculated as
,
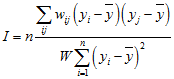where yi
is the value of the variable at the ith location, n
is the number of points, wij is a weight
indicating something about the spatial relationship of points i
and j, 
indicates
the double sum over all i and
all j where i ≠ j,
and 
, the sum of the values
in the weight matrix. Moran’s I
is akin to a correlation coefficient, as it is based on a product moment
formulation. I will usually range
from 1 to –1, with an expected value of 
; for large
n, this is approximately zero.
Positive values of I indicate
positive spatial autocorrelation, negative values negative spatial autocorrelation
(thus the popularity of the metric).
Assuming that the observed data could be randomly permuted across all of the observed locations, the variance of I can be estimated as
,
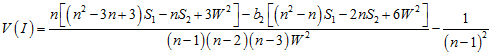where
,
,
and 
are the sums of the ith
row and ith
column of the weight matrix, respectively, and
.
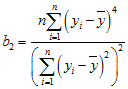Instead, one might assume that the data comes from an infinite, normally distributed population; in this case the variance can be estimated as
.
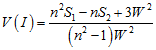Generally, the random assumption is considered more realistic.