Given a distance matrix and a connection scheme, this procedure finds the shortest path distance among all pairs of points. The result is an n × n distance matrix, where n is the number of points, and each value in the matrix, dij, represents the minimal sum of the distances traveled along the network, defined by the connection matrix, between points i and j.
| Menu: | Create→Distances→Geodesic/Shortest Path |
| Button: | |
| Batch: | GeodesicDists |
Beyond simple shortest path distances, this method can also be used to approximate geodesic distances in multi-dimensional space. Multi-dimensional data space is often curved rather than Euclidean; the simplest example of this is when points are found on the surface of a sphere. The distance among the points are best measured along the surface of the sphere rather than the direct measure through the sphere. For most data sets, however, it is impossible to know the curvature to properly measure the distance along the spatial surface. However, distances can be estimated along this curvature using approximate geodesic distances.
Approximate geodesic distances work by assuming that the distance between points which are close together can be approximated by Euclidean distance (because the effect of the curvature will be minimal). Points which are farther apart can have their distance estimated by summing the distances of a path connecting them through other points; thus, the curvature of the space (and the distance along it) can be approximated through a network connecting neighbors or close points to each other.
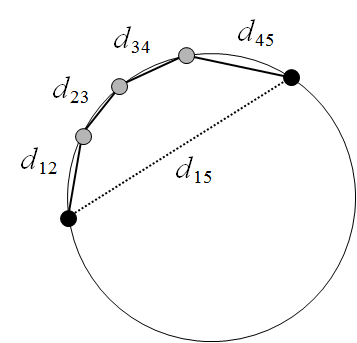
Example of approximate geodesic distances in two dimensions. Euclidean distance between points the black points (d15, represented by the dotted line) does not accurately reflect the distance between these points along the curvature of space (in this case, the circle). The approximate geodesic distance is the sum of the distances along the connection network (the solid straight lines): d12 + d23 + d34 + d45.
Given a predetermined connection scheme and a set of Euclidean distances among points, the approximate geodesic distance between a pair of points i and j is found as the shortest path between points i and j.
Geodesic/Shortest-Path Distance window.