This function will create a binary matrix representing specific connections (or relationships) among data locations in PASSaGE, as well as offering the option of constructing a tessellation matrix.
| Menu: | Create→Other→Connections/Tessellations |
| Button: | |
| Batch: | CreateConnect |
There are a number of methods by which one may connect points in space. The first of these is based simply on distance. Most of the other methods are hierarchical with respect to connectivity: nearest neighbors are minimally connected but do not necessarily represent a spanning network; a minimum spanning tree is the complete network with the minimal sum of the connection lengths; and so on, ending with the Delaunay tessellation, which produces the greatest connectivity of the methods presented here. All of these methods theoretically apply to one-dimensional patterns, but any connection scheme from minimum spanning tree onward will result in the identical result: every point is connected to its immediate neighbors. Most of the methods apply to both two- and three-dimensional patterns, with the exception of the least diagonal network, which only applies to two-dimensional data.
Most of these methods determine the connections based on a distance matrix rather than on the coordinates of the locations themselves. Therefore, one might choose to apply these methods to distances derived from non-location data in order to represent relationships among multivariate data points (a common use of minimum spanning trees).
These procedures have just a few options. The primary option is the specification of the desired connection scheme. Distance-based connections also requires entry of minimum and maximum values upon which to create connections. Most connection methods require only a distance matrix. The exceptions are the Delaunay/Dirichlet Tessellation and the Least Diagonal Network, both of which require both a distance matrix and a corresponding coordinate matrix. When determining a Delaunay/Dirichlet tessellation, you also have the option of producing a binary connection matrix, the tessellation matrix, or both.
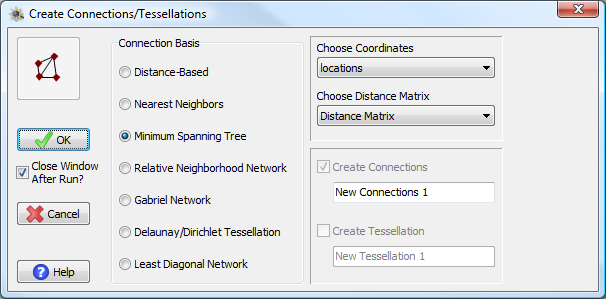
The Create Connections/Tessellations window.
The specific connection schemes are described in the following sections. We will use the point locations of 355 cancer registration districts from part of Western Europe as the input data for a running example.