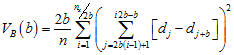 .
.These methods are designed for one-dimensional arrays of contiguous data; the general term for this in ecology would be a transect.
Blocked Quadrat Variance (BQV) was the original method designed for analyzing contiguous quadrats (Greig-Smith 1952); Kershaw (1957) suggested an adaptation for transects. This method calculates the variance of non-overlapping blocks of different sizes. This method requires the block sizes to scale by powers of 2 (e.g., 1, 2, 4, 8, 16…) and is very limited by this restriction. The variance for block size b is calculated as
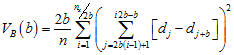 .
.
The scale at which the variance peaks is interpreted as the scale of the investigated pattern. Because the block sizes must scale by powers of two, the actual maximum scale used by PASSaGE with this method equals the largest power of two below the product of the chosen percentage and the length of the transect. For example, for a transect consisting of 100 quadrats with the maximum scale set to 50%, the largest power of two below 50% of 100 (=50) is 32.
Another problem with BQV is that it will not use all of the available data if the length of the transect is not exactly a power of two. In addition, BQV can be very sensitive to starting location (Errington 1973; Usher 1969); starting an analysis at a different quadrat could lead to very different results. Stepped Blocked Quadrat Variance (SBQV) is a method that tries to avoid this problem by averaging the results of multiple BQV analyses starting with a different quadrat each time (Usher 1969). Also, by sliding the starting position one is able to use all of the available data. The variance for SBQV is calculated as
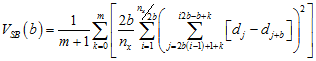 ,
,
where m is the number of extra quadrats available for the sliding window, i.e., the difference between the total number of quadrats and the maximum scale that can be tested. In the example above (a transect consisting of 100 quadrats with the maximum scale set to 50%), m = 50 – 32 = 18.
Neither of these methods is recommended for most analyses (other transect methods tend to perform better), but they are included in PASSaGE for completeness and comparative purposes.
The local quadrat variance methods were originally developed by Hill (1973). They differ from BQV in that their variances are based on overlapping blocks. There are two common forms of this method, Two-Term Local Quadrat Variance (TTLQV) and Three-Term Local Quadrat Variance (3TLQV).
TTLQV essentially calculates the mean square difference between adjacent blocks for each scale. The variance at block size (scale) b is
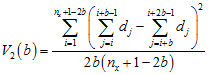 .
.
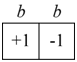
Logical template for TTLQV. The value in one block of width b is contrasted against the value in the following block, also of width b.
3TLQV is similar, except that it is based on three blocks, rather than two. This method looks at the squared difference between the sum of the first and third blocks and twice the second block (the second block is multiplied by two so that the expected value if all blocks were equal is zero). The variance of 3TLQV is
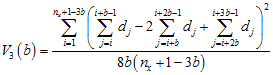 .
.
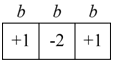
Logical template for 3TLQV. The value in the center block (of width b) is contrasted against the sum of the values of the blocks of width b to either side of it. The value in the center block is multiplied by two to counter the fact that it is measured over half of the area as the value found by summing the outer blocks.
For both methods, the scale at which the variance peaks is interpreted as the scale of the pattern being investigated.
Although the two methods are similar, 3TLQV has several advantages. First, it is less sensitive to global trends (nonstationarity) in the data (Lepš 1990). Second, peak drift (i.e., the difference between the true scale of the phenomenon and the observed peak) is less for 3TLQV than for TTLQV (Dale and Mah 1998; Dale 1999).
Paired Quadrat Variance (PQV) differs from BQV and the local quadrat variances in that it tests for scale by changing the distance between tested quadrats without increasing block size. The formula for PQV is
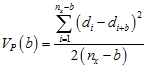 .
.
![]()
Logical template for PQV. Two blocks of size 1 are contrasted; unlike most of the other quadrat variance methods, the scale is modified by changing the distance between the blocks rather than changing the block size.
As with the above methods, peaks in variance are interpreted as the scale of pattern. PQV is essentially identical to a semivariogram analysis and is closely related to the calculation of autocorrelation (Dale and Mah 1998; ver Hoef et al. 1993).
Goodall (1974) was concerned with the lack of independence between measures at separate scales, because the same points are used over and over again in each calculation. To confront this, he suggested using each point in only a single scale, by picking pairs at random, assigning them to the appropriate scale and removing the individual points from the pool from which the next pair is chosen. This procedure, known as Random Paired Quadrat Variance (RPQV), is very limited by the amount of data available (Dale 1999; Ludwig and Goodall 1978) and tends to lack precision. A transect with 200 quadrats can produce only 100 pairs to divided among all the tested scales. If one wished to test all scales from 1 to 50, only 2 pairs would be used to estimate the variance at each scale (and this is an average, since some distances would have more than two and others would have zero).
Dale (1999) proposed a variation of paired quadrat variance called Triplet Quadrat Variance (tQV). This method is akin to PQV in the way 3TLQV is akin to TTLQV. Rather than looking at pairs separated by a set distance as in PQV, tQV examines triplets. The formula for tQV is
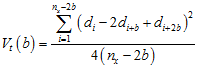 .
.
![]()
Logical template for tQV.
This is a rather new method and its properties have not been thoroughly examined.
Galiano (1982) proposed a pair of methods (a two term and a three term method) for detecting the patch size rather than the scale of pattern. These methods calculate the average size of either gaps or patches (whichever is smaller); the previously described quadrat variance methods average across both gaps and patches (Dale 1999). Galiano’s methods, known as New Local Variance (NLV), are closely related to TTLQV and 3TLQV. The NLVs calculate the differences among neighboring TTLQV (or 3TLQV) blocks. The variance for the two-term version of NLV is
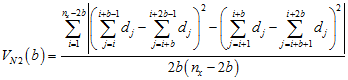 .
.
For the three-term version,
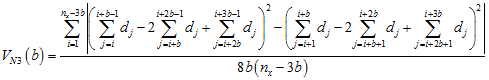 .
.
See Galiano (1982) and Dale (1999) for more information on these methods.