Quadrat covariance methods are very similar to quadrat variance methods. Instead of examining the quadrat variance of a single variable, one may be interested in the covariance of two variables. Every quadrat variance method described so far can be adapted to a covariance equivalent. In all cases the numerator contains a squared difference between one block and one or more other blocks; the general form of the numerator is therefore
![]() ,
,
where x and y indicate the two types of blocks being contrasted. For a covariance study, there are two variables A and B. Instead of squaring the difference of one variable, we multiply the difference of the pair, thus the numerator becomes
![]() .
.
Otherwise the formulas and logic are exactly identical to those for the quadrat variance methods. Note that the covariance of a variable with itself is the variance. Although not used by PASSaGE due to computational inefficiency, an alternate way to determine covariance is as follows: if VA is the quadrat variance for variable A, VB is the quadrat variance for variable B, and VA+B is the quadrat variance for the summed values of variables A and B (that is, the values when corresponding quadrats are summed), then the covariance can be calculated as
![]() .
.
| Menu: | Analysis→Contiguous Data→QuadVar→Quadrat Covariance Methods |
| Button: | |
| Batch: | QuadCovar |
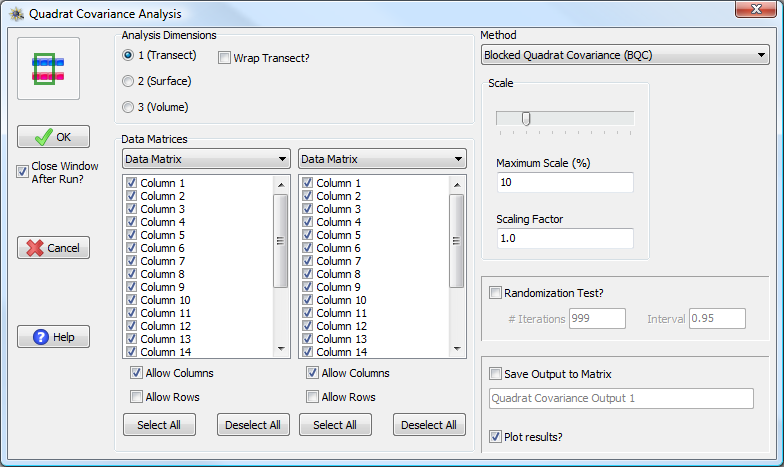
Quadrat Covariance Analysis window
All of the options for quadrat covariance methods are essentially identical to those from quadrat variance methods, except that the data come from two matrices rather than one. If all of the data one wishes to estimate covariances for is contained within a single data matrix, one can specify the same matrix for both sides of the contrast. Covariances are calculated between all of the possible pairs generated between data selected from the first matrix vs. data selected from the second matrix.
Permutation tests for quadrat covariance methods are slightly more complicated than those for quadrat variance methods; for covariance analysis the corresponding elements must be permuted in tandem. That is, one does not want to independently randomize the order of the two data matrices; rather, one rearranges them exactly the same way. This maintains the relationship between the variables at the level of individual measurements and allows us to use the randomization procedure to test the spatial covariance. Also, the null distribution of a covariance analysis should be examined as a two-tailed distribution, while a typical quadrat variance distribution can be thought of as one-tailed.