.Spectral analysis describes spatial pattern by fitting continuous wave forms to the data (Ripley 1978); the relative magnitudes of the coefficients of the fitted waves with different periods allows one to infer spatial scale. Traditionally, spectral analysis uses sine and cosine waves, although many other shapes are possible. Spectral analysis is somewhat similar to wavelet analysis except that in wavelet analysis the “wave” template only covers a single period while in spectral analysis the “wave” template is continuous.
Spectral analysis uses a pair of wave functions g1(v) and g2(v) with a periodicity of 2π (referred to as odd and even waves). These functions are identical except for phase:
.
The most commonly used wave functions are simply the sine and cosine waves; however other shapes are possible, including square, triangular, trapezoidal, three-value function, and sawtooth waves (Wei and Chen 1998; Wei et al. 1999; Wei 1999, 2000a, 2000b; Wei and Zhang 2000). Choice of a wave function should be based on assumptions about the shape of the underlying signal. Generally, one will most likely want to use the sine wave. The square wave may be particularly useful for analyzing presence/absence or other binary data; although functionally similar it is not identical to the more commonly known Walsh transform. The other wave forms may be less useful for spatial analysis, but have potential in certain types of electronic signal analysis where signals may take a variety of shapes (Wei and Chen 1998; Wei et al. 1999; Wei 1999, 2000a, 2000b; Wei and Zhang 2000).
In one-dimensional spectral analysis, the observed values are estimated as
,
where 
is the mean data
value, and cp
and sp
are the spectral coefficients for period p.
The spectral coefficients are estimated as:
.
The periodogram, Ip, is then calculated as
.
Two- and three-dimensional spectral analysis is quite similar (Dale 1999; Ford and Renshaw 1984; Renshaw and Ford 1984):
Two dimensions
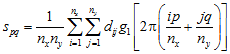
Three dimensions
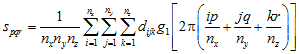
(the functions for c are identical to s except for the use of wave function g2).
Spectral analysis assumes evenly repeating patterns (periodicity), which are often not found in real data. The results can be very difficult to interpret compared to other methods and are often strongly affected by the choice of smoothing operation (Dale 1999; Usher 1975).
Information on R-spectrum, Theta-spectrum, etc…