Wavelet analysis is similar to many of the quadrat variance methods already discussed, although in some ways it is much more flexible. Wavelets have been heavily studied in mathematics and engineering for signal analysis and data compression, but have had limited use in biology (Bradshaw and Spies 1992; Bradshaw and McIntosh 1994; Dale and Mah 1998; Nakken 1999).
For our purposes, a wavelet function g(r) is a scalable windowing function whose integral over all r equals zero. One way to think of this is that the wavelet function describes a template (see below) that can be scaled to a desired size, then slid along the transect. When the template fits the observed data well, the value of the wavelet transform at that position is high; when it does not, the value is low. The wavelet transform at position px for scale bk is equal to
![]() ,
,
where d(p) is the value of the data at position p and f(px,pi) is the displacement between positions px and pi (the displacement is the signed distance, i.e., it can be negative). For two- and three-dimensions, the formulas are very similar:
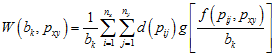
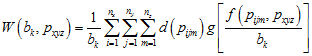 .
.
The overall variance for a given scale is
![]() ,
,
or the average of the squared wavelet transforms at all positions, while the overall variance for a given position is
![]() ,
,
or the average of the squared wavelet transform over all scales (m is the total number of measured scales). V and P for two- and three-dimensions are based on the same logic, being the average of the squared wavelet transforms for all positions or all scales, respectively. Although this seems complicated, it is simpler than it looks. In fact, it is extremely similar to the local quadrat variance methods. Two of the specific wavelet functions in PASSaGE are virtually identical to TTLQV and 3TLQV, differing only by a scalar multiplier.
There are numerous wavelet functions, g(r), that may be used for data analysis. For one-dimensional data, PASSaGE currently allows you to choose among five wavelet functions.
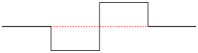
| Haar Wavelet | ||
| g(r) = | –1 if –1 ≤ r < 0 1 if 0 ≤ r < 1 0 otherwise |
 |
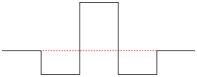
French Top Hat Wavelet |
||
| g(r) = | -1 if
2 if
0 otherwise |
 |
| Mexican Hat Wavelet | ||
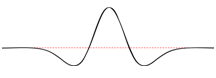 |
||
| Morlet Wavelet | ||
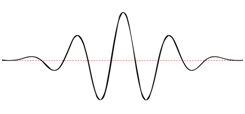 |
||
| Sine Wavelet | ||
| g(r) = | sin(πr) if 0 otherwise
|
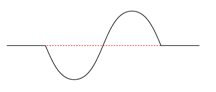 |
One-dimensional wavelet functions.
The simplest is known as the Haar (1910) wavelet. It is a square wavelet function and is essentially identical to TTLQV (Dale and Mah 1998); it compares the values of neighboring blocks of the same size. The wavelet identical to 3TLQV is known as the French Top Hat wavelet. A pair of more complicated wavelets are known as the Mexican Hat wavelet and the Morlet wavelet (after Daubechies 1992). Unlike the previous wavelets, these wavelets are continuous functions, leading to certain mathematical advantages. The Morlet wavelet is a complex function; only the real portion is used in the analysis. Finally, there is a wavelet based on a single cycle of a sine wave. Analyses which use full sine waves fall under spectral analysis.
PASSaGE has three wavelet functions for two- and three-dimensional data, all based on the logic of the Haar and French Top Hat wavelets. Each contrasts a pair of nested circles (in two dimensions) or sphere (in three dimensions). For two dimensions, this can be visualized as taking the Haar or French Top Hat wavelet and spinning it around its axis. The catch is that the “height” of the inner and outer parts needs to be altered such that the integral of the function will equal zero. There are many ways this could be done; three alternate approaches are provided here. In all three cases values within the outer circle (sphere) are given a value of -1. The variation comes from choice of the relative radii and the scalar multiplier for data contained within the inner circle (sphere). In the first approach, the radius of the outer circle (sphere) is set to double that of the inner circle (sphere). In the second approach, the radius of the outer circle (sphere) is set to 1.5 times the radius of the inner circle (sphere); this estimates data over a narrower range and reduces the magnitude of the multiplier for data within the inner circle (sphere). The final approach sets the magnitudes of the multipliers of the inner and outer data as equal (in this case -1 and + 1) and adjusts the radius of the outer circle (sphere) accordingly; this approach was conceived by Mark Dale (for the two-dimensional case, he christened this the “Boater” wavelet).
The formulas for the wavelets for each of these approaches in two and three dimensions are:
| Approach | 2D | 3D | |||
| Tall Top Hat Wavelet | Wide Spherical Wavelet | ||||
| 1 | g(r) = |
–1 if 1 ≤ r < 2
3 if 0 ≤ r < 1 0 otherwise |
g(r) = |
–1 if 1 ≤ r < 2
7 if 0 ≤ r < 1 0 otherwise |
|
| Short Top Hat Wavelet | Medium Spherical Wavelet | ||||
| 2 | g(r) = |
–1 if 1 ≤ r < 1½
1¼ if 0 ≤ r < 1 0 otherwise |
g(r) = |
–1 if 1 ≤ r < 1½
2⅜ if 0 ≤ r < 1 0 otherwise |
|
| Boater Wavelet | Narrow Spherical Wavelet | ||||
| 3 | g(r) = |
–1 if 1 ≤ r < 1 if 0 ≤ r < 1 0 otherwise |
g(r) = |
–1 if 1 ≤ r < 1 if 0 ≤ r < 1 0 otherwise |
|
The relative shapes of the two-dimensional wavelets can be seen below. The comparative properties of these wavelets have not been thoroughly studied; because of the similarities in their shapes they may be expected to give similar results.
|
|
|
|
|
|
|
|
|
Diagram of two-dimensional wavelets. From left to right: Tall Top Hat Wavelet, Short Top Hat Wavelet, Boater Wavelet. The top row represents a side view, the middle row a top view (including the scalar value indicating the height), and the bottom row a 3D representation of each wavelet. The wavelets are scaled such that the center circle had the same area.
In addition, there is a 2D version of the Mexican Hat Wavelet known as the Sombrero wavelet. Its formula is
.