These methods are (for the most part) based on expansions of one-dimensional quadrat variance methods to two-dimensions. They are designed for the analysis of contiguous surfaces.
This is the original quadrat variance method proposed by Greig-Smith (1952). It suffers from all of the problems of BQV for transects, as well as additional ones due to the limitations on the necessary rectangular shape of certain block sizes (e.g., a block size of 8 must be 2 × 4) (Dale 1999; Pielou 1977). Because of these limitations, PASSaGE does not currently calculate BQV for surfaces.
The local quadrat variance methods for surfaces are extensions of the methods for transects. The 2D version of TTLQV is known as Four-Term Local Quadrat Variance (4TLQV) and the 2D version of 3TLQV is known as Nine-Term Local Quadrat Variance (9TLQV) (Dale 1990, 1999).
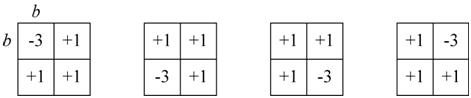
4TLQV calculates the mean square difference between one quarter of a square of size 2b and the other three quarters of the square.

Examples of the potential block comparisons for a 4TLQV analysis. The value (multiplied by three) in one b × b block is contrasted against the value in three adjacent blocks, each b × b. Because the choice of which block to multiple by three is arbitrary, one repeats the analysis for all four possibilities and uses the average as the final value.
The variance at block size (scale) b, when comparing the upper left corner to the other three (the left-most example in the above figure), is:
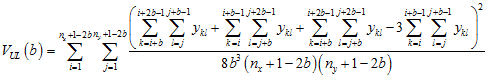 .
.
Because any of the four quarters could be compared to the others, one normally uses the average of the variances obtained from using each of the four quarters as the pivot. The formulas for VUR, VLL, and VLR are similar to that of VUL (where UL, UR, LL, and LR refer to upper left, upper right, lower left, and lower right, respectively). The formula for 4TLQV is then
![]() .
.
9TLQV is similar, except that it is based on the contrast of the center square of a 3x3 grid to the sum of the 8 outer squares.
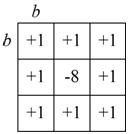
Logical template and block comparisons for 9TLQV. The value in the center b × b block (multiplied by 8) is contrasted with the 8 surrounding blocks.
The variance of 9TLQV can be calculated as
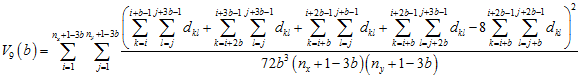 .
.
Note that this is a correct, but shortened, version of the equation; normally there would be nine separate double summations in the numerator (one for each block), but some of them were combined for compactness of presentation (see Dale 1999 for a complete description).
In general, 9TLQV should have the same sorts of advantages over 4TLQV as 3TLQV has over TTLQV (Dale 1999).
The two-dimensional equivalent of triplet quadrat variance (tQV) is pentuplet quadrat variance (5QV). This method looks at sets of 5 quadrats, a center block and the 4 quadrats separated from it by the test distance in each of the 4 cardinal directions (Fortin and Dale 2005). The variance can be determined as
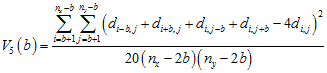 .
.
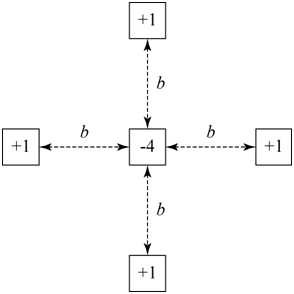
Logical template for 5QV.