These methods are designed for the analysis of contiguous volumes; they are based on expansions of the two-dimensional methods.
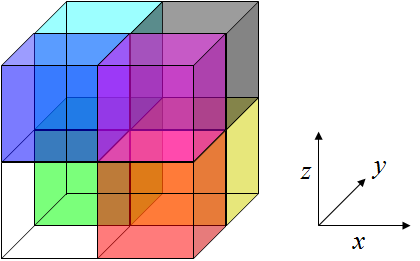
The local quadrat variance methods for two dimensions can logically be extended to three dimensions. The “two-term” equivalent is to extend the squares of 4TLQV into cubes in three dimensions, leading to an eight cube system or 8TLQV.

Example of the block comparisons for an 8TLQV analysis. Each of the eight blocks has been assigned a different color in order to highlight the layout. The relative coordinate positions of the eight blocks is: White = [1,1,1], Red = [2,1,1], Green = [1,2,1], Blue = [1,1,2], Yellow = [2,2,1], Magenta (Pink) = [2,1,2], Aqua = [1,2,2], and Black = [2,2,2].
Let sb(x,y,z) be the sum of the values in the b × b × b cube starting at position x, y, z. Therefore,
![]() .
.
Given quadrat (x, y, z), the eight blocks can be numbered as 1 or 2 on each axis (above figure), leading to:
As in 4TLQV, one block must serve as the pivot block with respect to the others. We define SP as the sb of the pivot block and SO as the sum of sb for all blocks other than the pivot. This being the case, the 8TLQV variance for the pivot block is
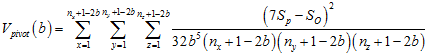 ,
,
where nx is the size of the volume along the x-axis, ny is the size of the volume along the y-axis, nz is the size of the volume along the z-axis. Because all 8 blocks can serve as the pivot (choice of any specific one is arbitrary), we must average Vpivot(b) for all 8 possibilities, thus the 8TLQV variance is calculated as
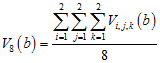 .
.
Just as 4TLQV can be extended into three dimensions to form 8TLQV, 9TLQV can be extended into three dimensions to form 27TLQV. The 27-term local quadrat variance can be pictured as a block of 27 cubes, much like a Rubik’s Cube.
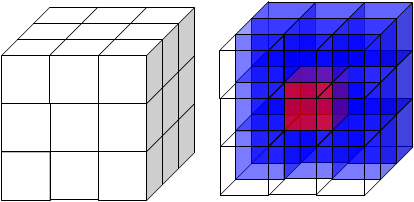
Example of the block comparisons for a 27TLQV analysis. The left figure shows the solid Rubik’s Cube-like set of blocks. The right figure highlights the center block [2,2,2] in red.
Using the same notation as above, the variances for each of the 27 blocks is as follows:
For 27TLQV, the center block [2,2,2] (the red block in the above figure) is contrasted with all other blocks. In this case SP = sb[2,2,2] and SO is the sum of all blocks except [2,2,2], thus the variance is
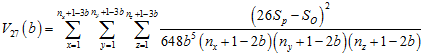 .
.
The three-dimensional equivalent of triplet quadrat variance (tQV) and pentuplet quadrat variance (5QV) is septuplet quadrat variance (7QV). This method looks at sets of 7 quadrats, a center block and the 6 quadrats separated from it by the test distance in each of the 6 cardinal directions. The variance can be determined as
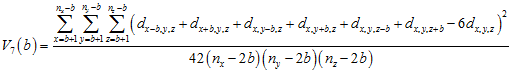 .
.
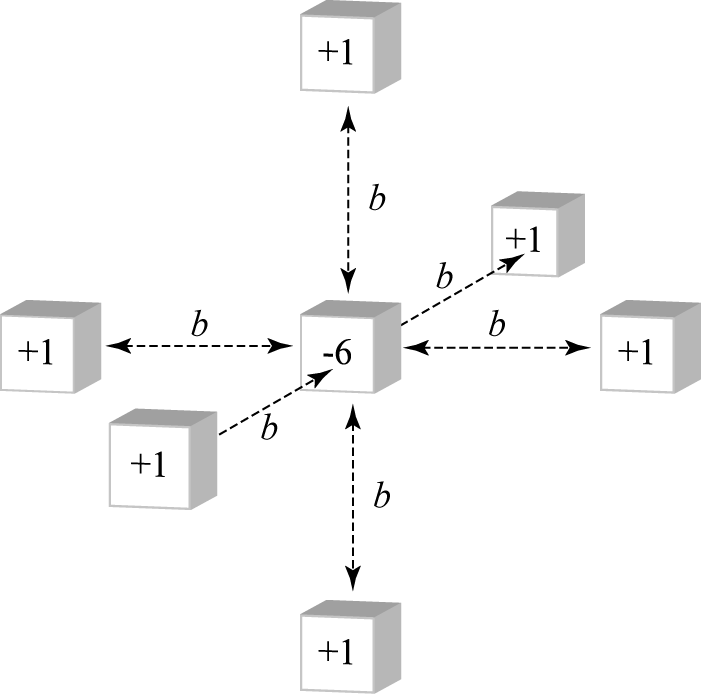
Logical template for 7QV.